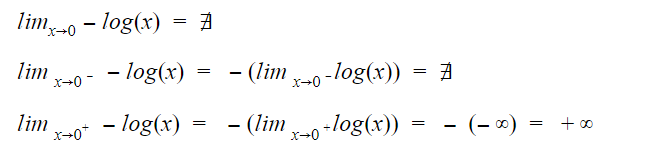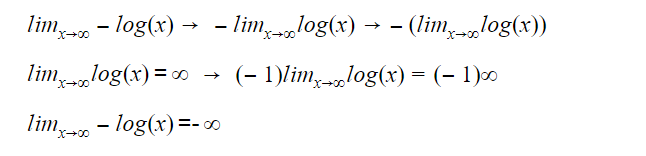pH
[H3O+] é concentração em mols de H3O+ dissociados em solução
pH= - Log_10 [H3O+]
pH = f(x)
[H3O+] = x
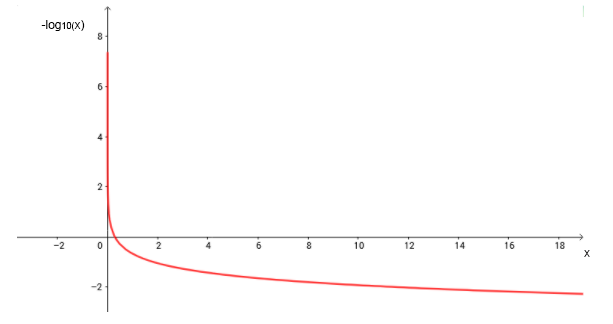
f(x)= - Log_10 (x)
D(f)= {x ∈ R, x>0}
Im(f)= {f(x) ∈ R, - ∞ < f(x) < ∞ }



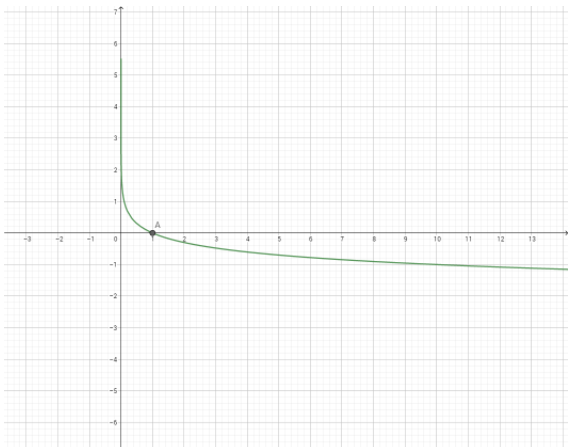
O valor de X que representa a concentração molar (mol/l) unidade de massa por volume, tem como domínio os reais positivos e não nulos, considerando que não pode existir uma quantidade negativa de massa ou de volume real.
A imagem varia de -(infinito) a +(infinito) representando a variação de pH, que aumenta infinitamente de acordo com o quanto a concentração de OH- é maior do que a de H3O+ em solução. E diminui infinitamente com o quão maior é a concentração de H3O+ em relação a OH-.
Considera-se pH em 7 quando as concentrações dos dois são praticamente iguais.

Concentração de H3O+
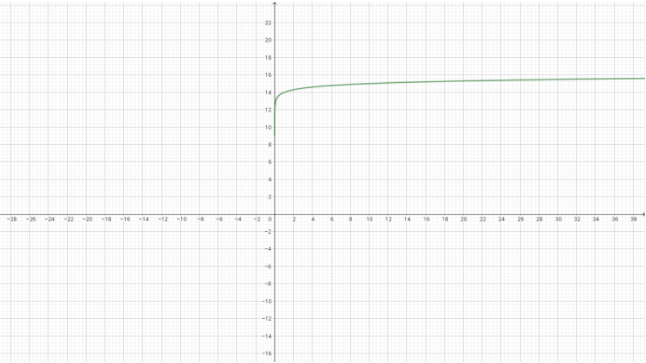
A função inversa lhe permite encontrar a concentração de H3O+ dissociados a partir do pH.
[H3O+] = 10^-pH
pH = x
[H3O+] = f^-1(x)
f^-1(x)=10^-x
D(f^-1)= {x ∈ R, -∞ < x <∞}
Im (f-1)= { f^-1(x) ∈ R, f^-1(x) > 0}

pOH-
O pOH determina a concentração de OH- dissociados em uma solução. Pode ser usado em uma função para determinar o pH com relação pH + pOH =14
pOH é encontrado da mesma maneira que o pH, mas usando concentração de OH- ao invés de H3O+.
pOH = - Log_10 [HO-]
pH = - (-Log_10[HO-]) + 14
h(x) = - (-Log_10(x)) + 14
D(h) = {x ∈ R, x>0}
Im(h) = {h(x) ∈ R, -∞ < h(x) <∞}

Periodicidade da Função

Função periódica: f(x) = f(x+p) , p ∈ lR*: para todo x ∈ lR
A função estudada não é periódica pois nela f(x) ≠ f(x+p) em p ≠ 0
- Log_10(x+p) ≠ - Log_10(x)
x+p ≠ x
p ≠ 0

Paridade da Função

Graficamente pode-se afirmar que não se trata de uma função par, pois não é simétrica com relação ao eixo y. Também não é ímpar, por não ser simétrica com relação a origem.

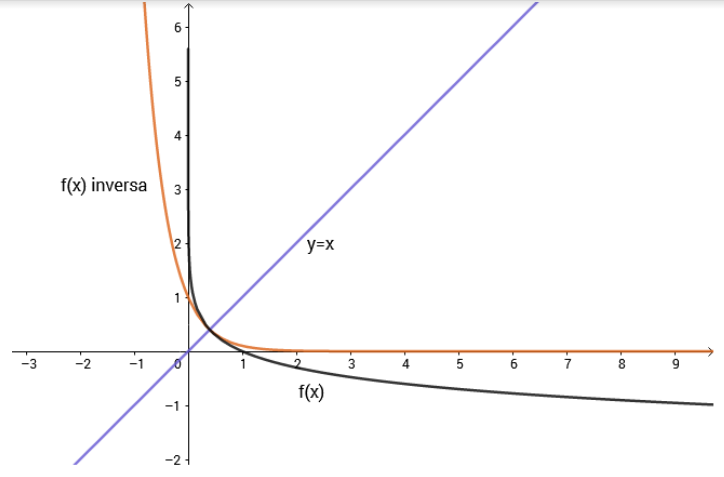
Bijetividade da Função

Uma função é bijetora caso ela seja injetora e sobrejetora.

Função Injetora: f(x1) ≠ f(x2) ⇒ x1 ≠ x2 ou f(x1) = f(x2) ⇒ x1 = x2.
f(x1) = -log_10x1 ⇒ -log_10x1 = y1 ⇒ x1 = 10-y1
f(x2) = -log_10x2 ⇒ -log_10x2 = y2 ⇒ x2 = 10-y2
x1 = x2 ⇒ 10-y1 = 10-y2 (Elementos de mesma base) ⇒ -y1 = -y2
Logo, a função é injetora.

Função Sobrejetora: f(x1)=f(x2) e para todo f(x) existe um Y.
f(x1) = -log_10x1 ⇒ -log_10x1 = y1 ⇒ x1 = 10-y1
f(10-y1) = -log_10(10-y1) = +y1 log_10(10) ⇒ +y1
Logo, a função é sobrejetora.

Portanto, a função é bijetora. Se uma função é bijetora, então tem uma inversa. Assim, a inversa da função estudada é:
y = - Log_k(x) ⇒ x = - Log_k(y)
k^-x = y ⇒ f^-1(x) = k^-x

Limites da Função

Para {x ∈ R, x>0}

Limite de x tendendo a zero



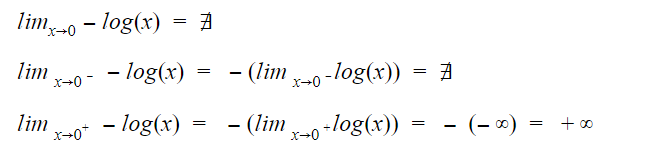
Considerando que o domínio da função pH segue a propriedade da função logarítmica que tem seu domínio no conjunto dos reais apenas em valores reais positivos e não nulos de x, para x tendendo a zero pelo lado positivo, o pH aumenta infinitamente em decorrência da redução infinita da concentração de H3O+,que no entanto, considerando que não pode existir uma quantidade negativa de massa ou de volume real, e que não é possível afirmar quantidade completamente inexistente de um composto, a concentração de H3O+ nunca será negativa ou nula.

Limite de x tendendo ao infinito



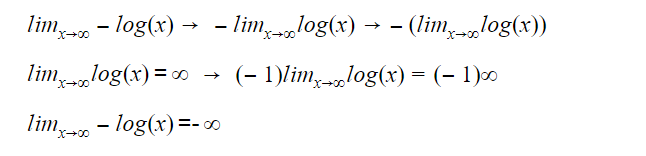
Quando a concentração de H3O+tende ao infinito o valor de pH tende a menos infinito, considerando valores de pH negativos para soluções extremamente ácidas.